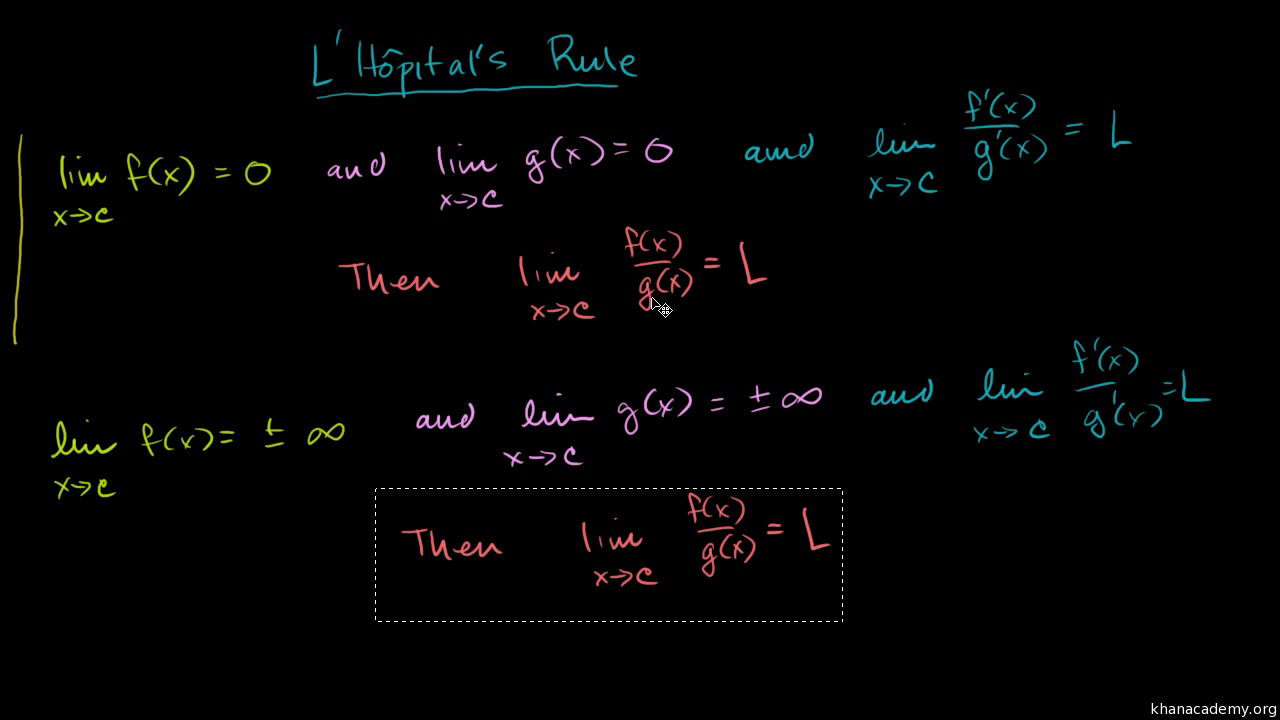L Hopital S Rule Proof Pdf

Proof of l hospital s rule theorem.

L hopital s rule proof pdf. L hopital s rule is a theorem that can be used to evaluate difficult limits. Suppose exist and 0 for all in an interval. The rule also works for all limits at infinity or one sided limits. Theorem 1 theorem l hôpital s rule assume that f x and g x are differen tiable on an open interval containing a and that f a g a 0 also assume that g x 0 for x near but not equal to a.

Proof of l hôpital s rule in the text we proved a special case of l hôpital s rule theorems 1 and 2 in ltsection 7 7 or et section 4 7. The proof of l hôpital s rule is simple in the case where f and g are continuously differentiable at the point c and where a finite limit is found after the first round of differentiation. L hospital s rule also spelled l hôpital s is a way to find limits using derivatives when you have indeterminate limits e g. The theorem states that if f and g are differentiable and g x 0 on an open interval containing a except possibly at a and one of the following holds.

Proof of macho l hˆopital s rule. By assumption f and g are differ entiable to the right of a and the limits of f and g as x a are zero. In those cases the usual ways of finding limits just don t work. It involves taking the derivatives of these limits which can simplify the evaluation of the limit.

Since these values agree with the limits f and gare continuous on some half open interval a b and differentiable on a b. Also 0 else 0 at some by rolle s theorem. Define then. L hospital s rule doesn t work in all cases.

Define f a to be zero and likewise define g a 0. If lim 0 lim and lim exists then lim lim.