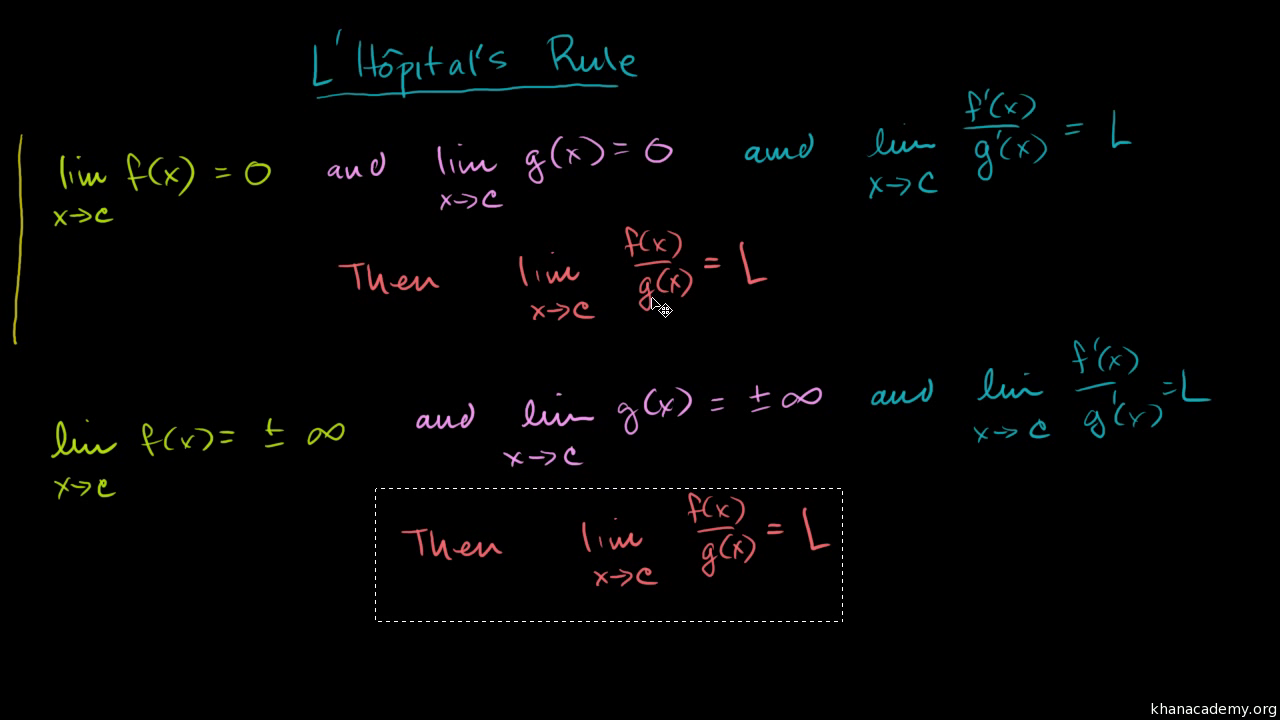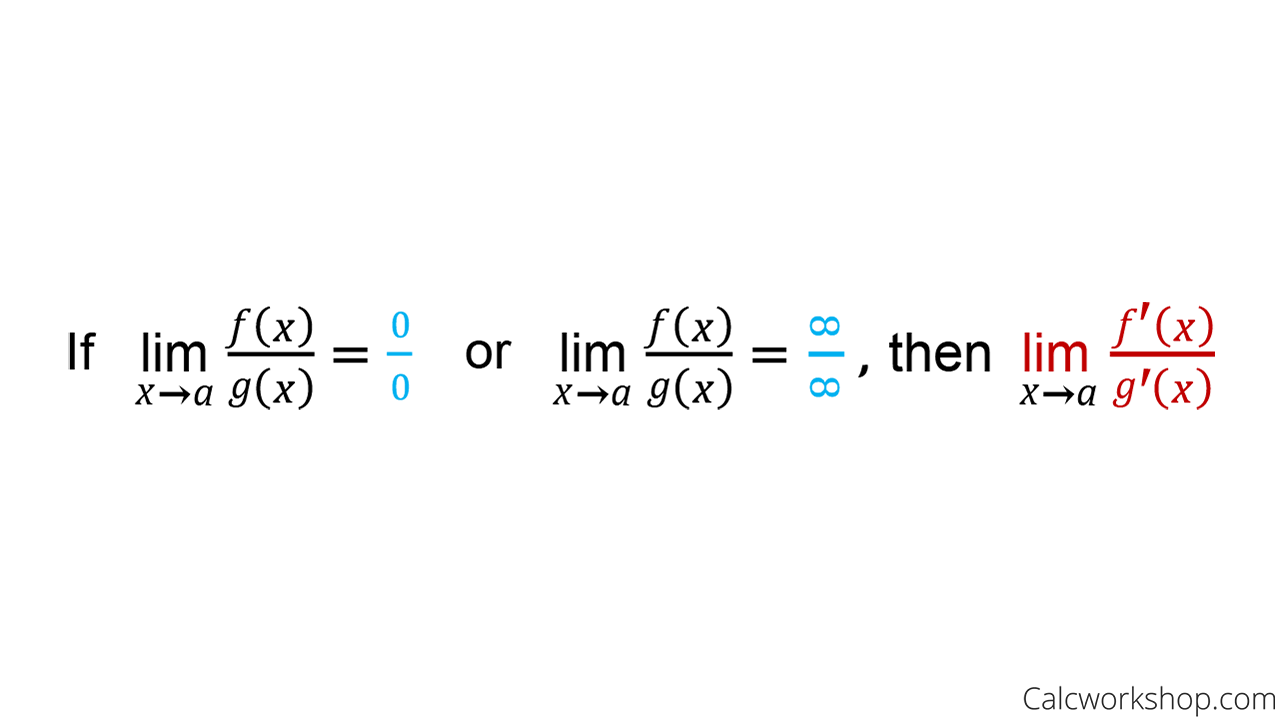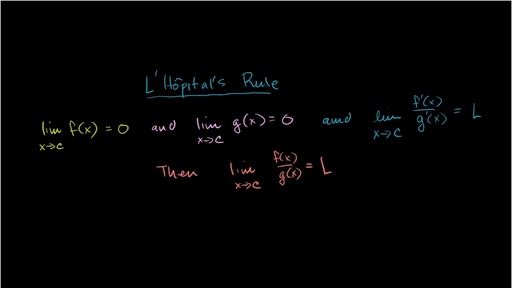L Hopital S Rule Infinity

And the denominator is approaching negative infinity.

L hopital s rule infinity. There are numerous forms of l hopital s rule whose verifications require advanced techniques in calculus but which can be found in many calculus books. It is used to circumvent the common indeterminate forms frac 0 0 and frac infty infty when computing limits. Both f x and g x have infinte limit either positive or negative as x approaches a. Also one of the following must hold true.

L hospital s rule also spelled l hôpital s is a way to find limits using derivatives when you have indeterminate limits e g. Instead of using l hopital s rule we could have multiplied both top and bottom by which is the conjugate of the numerator. If we apply l hopital s rule we get. Derivative of negative 3x squared is negative 6x.

For example find the limit at infinity of eˣ x. Find limits at infinity using l hôpital s rule. L hôpital s rule can help us calculate a limit that may otherwise be hard or impossible. L hospital s rule doesn t work in all cases.

The rule also works for all limits at infinity or one sided limits. So this is negative infinity. So let s apply l hopital s rule again. Infinity minus infinity return to the limits and l hôpital s rule starting page.

In mathematics more specifically calculus l hôpital s rule or l hospital s rule french. Often particularly with fractions l hôpital s rule can help in cases where one term with infinite limit is subtracted from another term with infinite limit. Which tends to infinity so the limit is. Negative 6 times infinity is negative infinity.

L hôpital is pronounced lopital who was a french mathematician from the 1600s. Is a theorem which provides a technique to evaluate limits of indeterminate forms application or repeated application of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. Let f and g be differentiable functions with g x not zero in an interval around a except possibly at a itself. So l hospital s rule tells us that if we have an indeterminate form 0 0 or infty infty all we need to do is differentiate the numerator and differentiate the denominator and then take the limit.

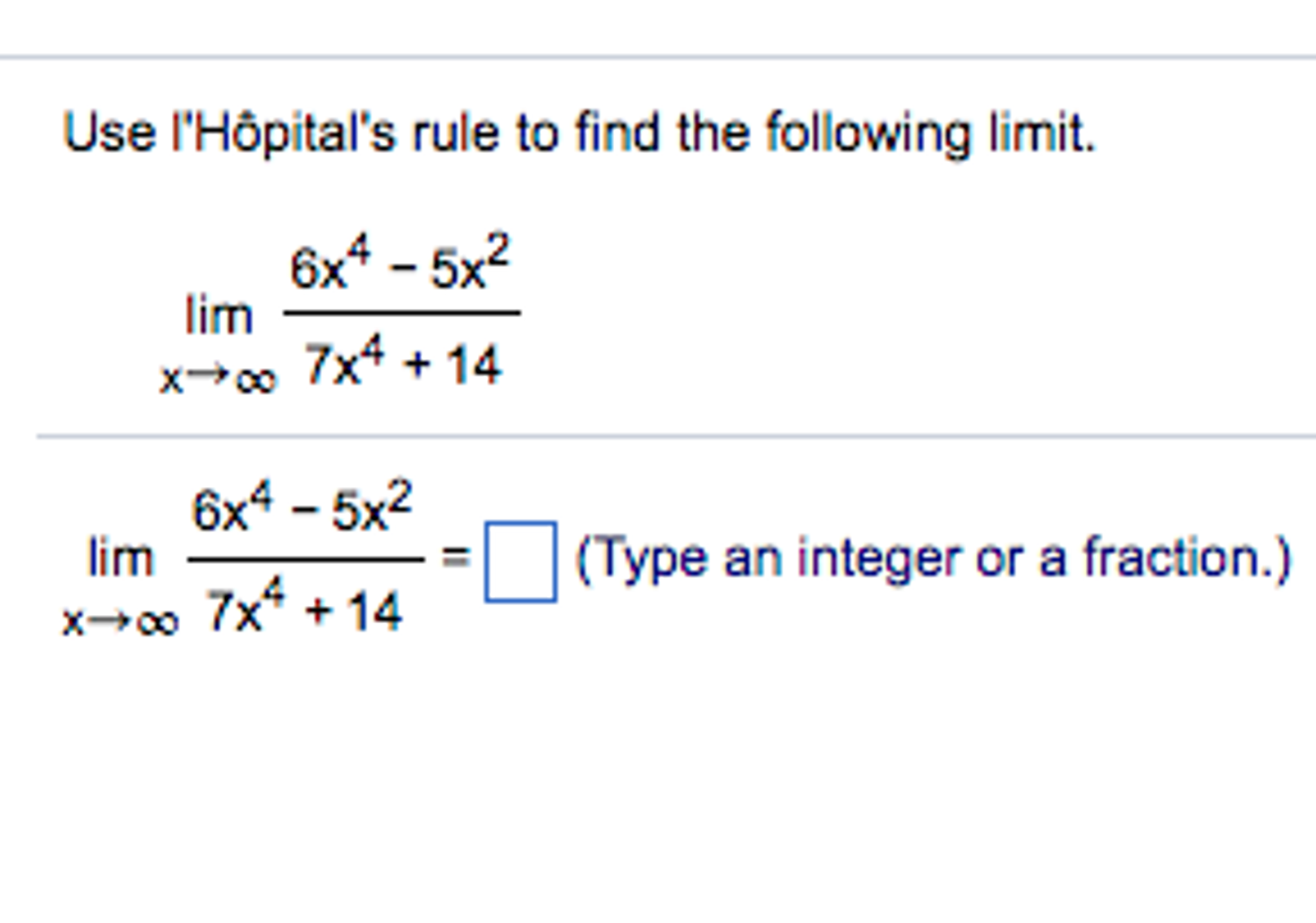
In those cases the usual ways of finding limits just don t work. If you re seeing this message it means we re having trouble loading external resources on our website. And once again when you evaluated infinity the numerator is going to approach infinity. The following problems involve the use of l hopital s rule.

This is generally done by finding common denominators. If we plug in x 4 we get 0 0 so when we apply l hopital s rule we get.